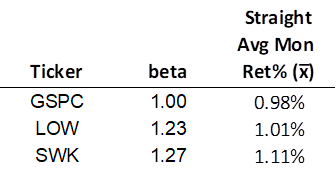
I thought it might be illustrative to look at two Dividend Kings with a nearly identical beta, but with very different average annual returns over the last five years (through July 2022): Lowe’s Companies Inc [LOW] and Stanley Black & Decker Inc [SWK].
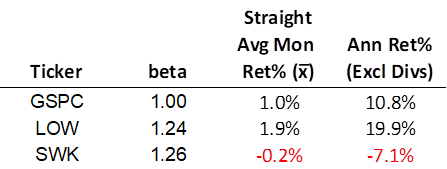
Beta says both companies were 25% more volatile relative to the market, but Lowe’s vastly outperformed the market (the S&P 500 Index, indicated by the ticker GSPC) and Black & Decker grossly underperformed the market. Please take my word; including the effect of dividends, reinvested or not, would not have materially affected the magnitude of the performance difference in these two stocks. As we’ll see, there’s more to beta than meets the eye.
First, let’s take a quick look at the scatter plots. The slope (beta) of the linear regression is nearly identical and there doesn’t appear to be any other standout differences.
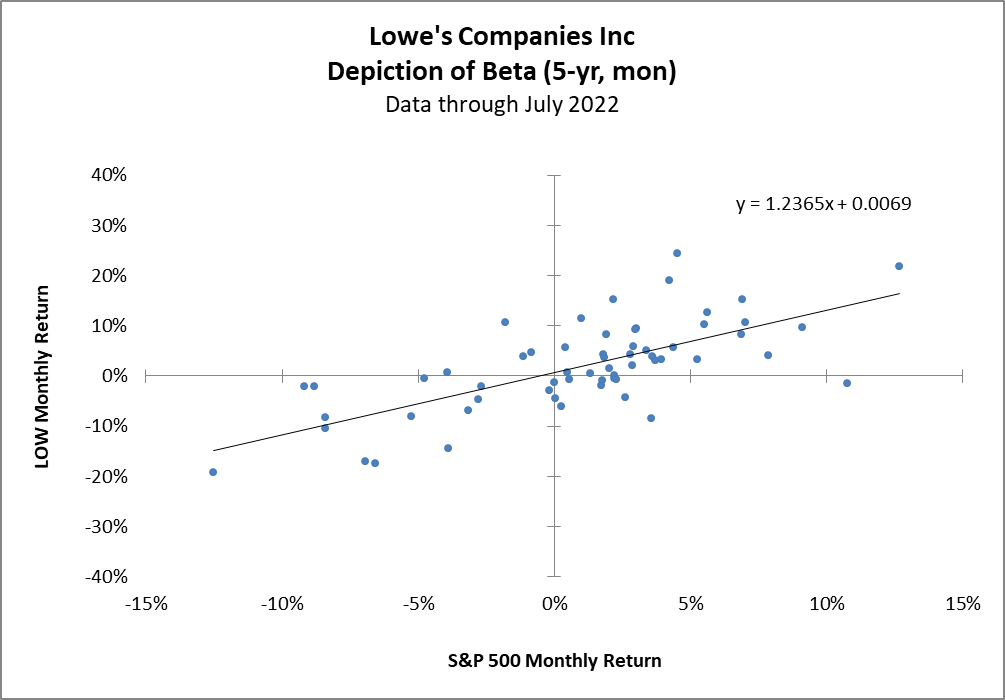
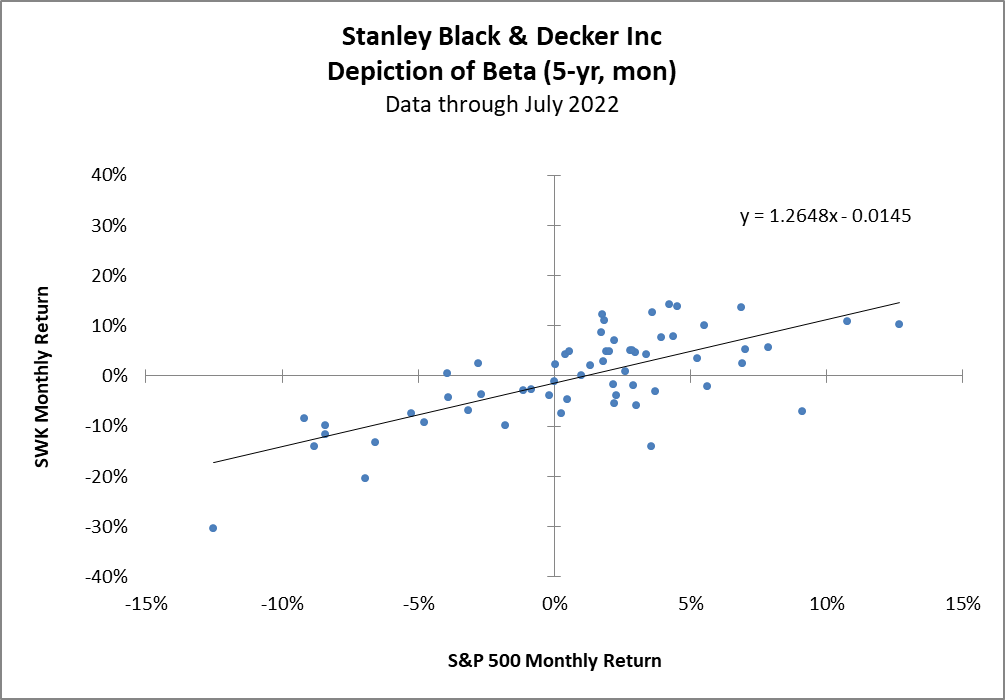
Disecting Beta
I used the tables from Method 1 in the first part of this discussion on beta to inspect the details that might explain this performance gap between LOW and SWK. There are nine months out of the 60 months that ‘explain’ how SWK performed so much worse, despite having the same volatility as LOW. Bear in mind, these were not SWK’s nine worst months, though three of the nine would make that list. Instead, these are the months were SWK underperformed LOW to the greatest degree. The right-most column presents that calculation. Note that it isn’t a simple difference, but a ratio of factors. The following months bubble to the top when we sort the 60-month period from smallest to largest.
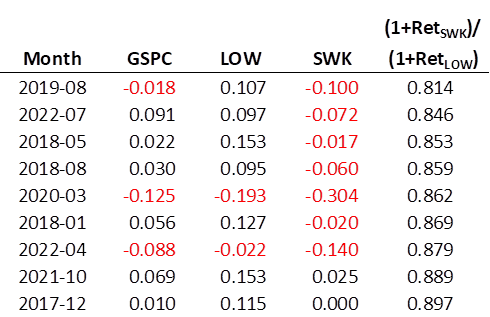
I say these months ‘explain’ SWK’s performance. However, what I really mean is that when these specific months are removed from the data set, SWK and LOW have similar returns over the time period. Now SWK looks to have the performance edge and their betas remain virtually unchanged.
I removed the average annual return column as it isn’t really relevant to a period where we play Jenga with the months. Aside from looking at just how much SWK underperformed LOW in the months above, note that these tended to be more extreme months, positive and negative, for the S&P 500. And this is the important point. How a stock performs in the more extreme months of the underlying index can have a greater effect on its overall return than on beta.
Not All Betas are the Same
It is my contention that beta shouldn’t be used to provide expectations about future returns. I’ve shown, at least anecdotally, that beta can be very inconsistent in explaining average annual returns even over the historical period on which it is based. Further, I’ve shown that two companies with similar beta can exhibit vastly different historical performance. Clearly, we cannot ascertain the reasons for historical performance differences by looking at point estimates. And dissecting beta and throwing out certain outlier months is impractical. However, what if there was a more objective, formulaic way to tease just a little more information out of beta?
I began to wonder what would happen if we split beta up and looked at what I refer to as ‘beta-‘ and ‘beta+’. The former is a calculation of beta using only the months where the index had a negative return; the latter uses only months where the return is greater than or equal to 0%. Might this give us insight into how a company will perform in future bad months? At a minimum, could it be used to explain past performance?
Asymmetric Beta
Here’s an expanded table for LOW and SWK.
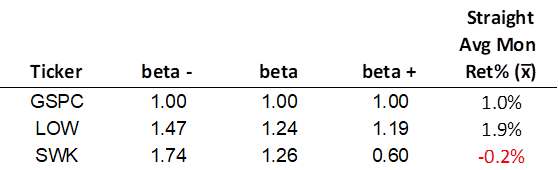
There may be some evidence here that illustrates why SWK performed so poorly despite a volatility that was not materially different than LOW, which performed so well. SWK was much more volatile when the market did poorly, than when it did well. Let’s remove the same nine months as before and see what changes.
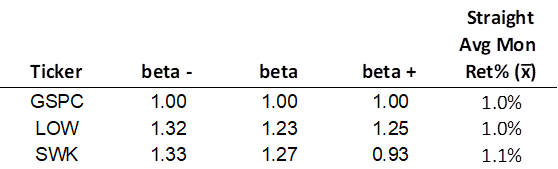
Removing the worst of the underperformance, has greatly reduced the skew towards higher volatility in the negative return months.
It isn’t exactly practical to calculate asymmetrical betas, even if they help explain historical performance. Studies of asymmetrical betas have drawn mixed conclusions about their utility. Beta was studied at length in 2019 in ‘Symmetric and Asymmetric Market Betas’, by Levi and Welch. Reading the paper isn’t easy; the abstract is as close to clarity as you’ll get.
Our paper explores whether a symmetric plain or an asymmetric down-beta is a better hedging measure (Roy 1952; Markowitz 1959). Unlike Ang, Chen, and Xing (2006) and Lettau, Maggiori, and Weber (2014), we find that the prevailing plain market beta is the better predictor, even for crashes. It also predicts the subsequent down-beta (i.e., beta measured only on days when the stock market had declined) better than down-beta itself. Stocks with higher down-betas ex ante also do not earn higher average rates of return ex post. Thus, down-betas are useful for neither hedging nor risk-pricing purposes.
So, in case you thought the secret to success is to find stocks with low down-betas (what I’ve been referring to as beta-), rest assured, it isn’t worth it.
If beta cannot be relied upon to develop expectations about future returns, what should we use it for?
Stay tuned for On Beta (Part 3 of 3).
